Mam takie zadanie:
Skrzaty
Limit pamięci: 64 MB
Zły smok Bitol najechał krainę skrzatów i wziął w niewolę jej mieszkańców. Przydzielił każdemu z  skrzatów inne stanowisko pracy i, samemu ległszy na stercie skradzionych kosztowności, jął leniwie nadzorować ich mozolne trudy.
skrzatów inne stanowisko pracy i, samemu ległszy na stercie skradzionych kosztowności, jął leniwie nadzorować ich mozolne trudy.
Jako że Bitol jest wyjątkowo gnuśnym smokiem, nie obserwuje jednocześnie wszystkich poddanych. Zamiast tego cały czas przygląda się uważnie tylko skrzatom pracującym przy pewnej grupie stanowisk. W tym czasie wszystkie nieobserwowane przezeń skrzaty mogą spotykać się oraz dowolnie zamieniać się miejscami (Bitol nie jest w stanie zapamiętać, przy którym stanowisku pracował który skrzat). Co godzinę smok obraca głowę i zaczyna obserwować inny podzbiór skrzatów.
Skrzat Bajtazyl, któremu smok przydzielił stanowisko 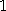 , chce zmobilizować towarzyszy niedoli do przeciwstawienia się Bitolowi. W tym celu musi najpierw spotkać się z sędziwym skrzatem Bajtomirem, któremu smok przydzielił stanowisko
, chce zmobilizować towarzyszy niedoli do przeciwstawienia się Bitolowi. W tym celu musi najpierw spotkać się z sędziwym skrzatem Bajtomirem, któremu smok przydzielił stanowisko  . Przed Bajtazylem stoi zatem wyzwanie: odpowiednio zamieniając się z innymi skrzatami miejscami, winien jak najszybciej doprowadzić do sytuacji, w której on sam, ani stanowisko przy którym stoi aktualnie nasz śmiałek, ani stanowisko
. Przed Bajtazylem stoi zatem wyzwanie: odpowiednio zamieniając się z innymi skrzatami miejscami, winien jak najszybciej doprowadzić do sytuacji, w której on sam, ani stanowisko przy którym stoi aktualnie nasz śmiałek, ani stanowisko  nie byłyby obserwowane przez smoka.
nie byłyby obserwowane przez smoka.
Twoim zadaniem jest ustalenie, kiedy najwcześniej może dojść do spotkania. Na szczęście wiadomo, że za 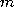 godzin smok uśnie i wówczas wszystkie skrzaty będą w stanie komunikować się swobodnie.
godzin smok uśnie i wówczas wszystkie skrzaty będą w stanie komunikować się swobodnie.
Wejście
W pierwszym wierszu standardowego wejścia znajdują się dwie liczby całkowite  i
i 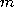 (
(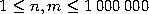 ) oznaczające odpowiednio liczbę skrzatów oraz liczbę godzin pozostałych do czasu, aż Bitol zaśnie. W następnych
) oznaczające odpowiednio liczbę skrzatów oraz liczbę godzin pozostałych do czasu, aż Bitol zaśnie. W następnych 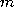 wierszach znajdują się opisy grup stanowisk obserwowanych przez smoka w kolejnych godzinach, po jednym w wierszu. Na opis
wierszach znajdują się opisy grup stanowisk obserwowanych przez smoka w kolejnych godzinach, po jednym w wierszu. Na opis 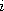 -tej grupy stanowisk składa się liczba całkowita
-tej grupy stanowisk składa się liczba całkowita 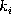 (
(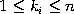 ) oznaczająca liczbę obserwowanych stanowisk oraz
) oznaczająca liczbę obserwowanych stanowisk oraz 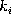 uporządkowanych rosnąco liczb całkowitych ze zbioru
uporządkowanych rosnąco liczb całkowitych ze zbioru 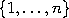 oznaczających numery obserwowanych stanowisk. Wszystkie liczby w wierszu poodzielane są pojedynczymi odstępami.
oznaczających numery obserwowanych stanowisk. Wszystkie liczby w wierszu poodzielane są pojedynczymi odstępami.
Możesz założyć, że 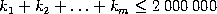 .
.
Wyjście
W pierwszym i jedynym wierszu standardowego wyjścia Twój program powinien wypisać jedną liczbę całkowitą ze zbioru 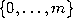 - najmniejszą liczbę godzin, po której Bajtazyl może dotrzeć do Bajtomira.
- najmniejszą liczbę godzin, po której Bajtazyl może dotrzeć do Bajtomira.
Przykład
Dla danych wejściowych:
5 4
3 1 3 4
2 3 5
3 1 2 3
2 1 2
poprawną odpowiedzią jest:
2
Dla danych wejściowych:
6 2
4 2 3 4 5
6 1 2 3 4 5 6
poprawną odpowiedzią jest:
0
Dla danych wejściowych:
10 4
1 1
2 9 10
7 1 3 4 7 8 9 10
2 1 10
poprawną odpowiedzią jest:
4
Wyjaśnienie do przykładu:
W pierwszym z powyższych przykładów podczas pierwszej godziny swej wyprawy Bajtazyl nie może opuścić stanowiska o numerze 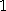 , gdyż jest ono obserwowane przez smoka. Podczas drugiej godziny może on zamienić się miejscami ze skrzatem przy stanowisku o numerze
, gdyż jest ono obserwowane przez smoka. Podczas drugiej godziny może on zamienić się miejscami ze skrzatem przy stanowisku o numerze  . Dzięki temu dopiero na początku trzeciej godziny smok Bitol odwróci głowę ku stanowiskom o numerach
. Dzięki temu dopiero na początku trzeciej godziny smok Bitol odwróci głowę ku stanowiskom o numerach 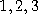 , a Bajtazyl będzie mogł spotkać się z Bajtomirem.
, a Bajtazyl będzie mogł spotkać się z Bajtomirem.
W drugim z powyższych przykładów do spotkania może dojść natychmiast, gdyż w pierwszej godzinie smok nie patrzy na stanowiska Bajtazyla i Bitomira.
W trzecim przykładzie do spotkania może dojść dopiero wtedy, gdy Bitol uśnie.
Znalazłem taki poprawny kod:
#include <cstdlib>
#include <cstdio>
#include <vector>
#include <iostream>
using namespace std;
struct przed {
int p;
int k;
};
int wbez(int a) {
if (a > 0)return a;
else return -1 * a;
}
bool czy_wsp(int *tab, int dl, vector<przed> prz[1]) {
int ltab = 0; // licznik tablicy
int lvec = 0; // licznik vectora
bool wynik = false;
int ostwprz = -1;
for (ltab; ltab < dl; ltab++) {
//DOBRA FUNKCJA
while (true) {
if (lvec == prz[0].size()) {
lvec--;
break;
} else if (tab[ltab] >= prz[0][lvec].p && tab[ltab] <= prz[0][lvec].k)
break;
else if (tab[ltab] < prz[0][lvec].p)
break;
if (ltab == 0)
wynik = true;
else if (-1 * tab[ltab - 1] != prz[0][lvec].k && tab[ltab - 1] < 0)
wynik = true;
else if (tab[ltab] > prz[0][lvec].k && tab[ltab - 1] < prz[0][lvec].k && tab[ltab - 1] > 0)
wynik = true;
lvec++;
}
if (tab[ltab] >= prz[0][lvec].p && tab[ltab] <= prz[0][lvec].k) {
if (tab[ltab] - 1 >= prz[0][lvec].p && ltab > 0)
if (tab[ltab] - 1 != tab[ltab - 1] * (-1))
wynik = true;
tab[ltab] *= -1;
}
}
if (wbez(tab[dl - 1]) < prz[0][prz[0].size() - 1].k) {
wynik = true;
}
for (int a = 0; a < dl; a++)
if (tab[a] < 0)tab[a] = 0;
return wynik;
}
void nzbior(int *tab, int dl, vector<przed> prz[1], int n) {
vector<przed> tym;
int ltab;
przed pom;
pom.p = 1;
for (int ltab = 0; ltab <= dl; ltab++) {
if (ltab == 0)
pom.p = 1;
else
pom.p = tab[ltab - 1] + 1;
while (ltab != dl && tab[ltab] == 0)
ltab++;
if (ltab != dl)
pom.k = tab[ltab] - 1;
else
pom.k = n;
if (pom.p <= pom.k) {
tym.push_back(pom);
}
}
prz[0].assign(tym.begin(), tym.begin() + tym.size());
}
int main(int argc, char *argv[]) {
int n, m;
scanf("%d%d", &n, &m);
int *dl = new int[m];
int **obs = new int *[m];
vector<przed> prz[1];
przed pom = {1, 1};
prz[0].push_back(pom);
int i;
bool wyn = false;
for (i = 0; i < m; i++) {
scanf("%d", &dl[i]);
obs[i] = new int[dl[i]];
for (int a = 0; a < dl[i]; a++)
scanf("%d", &obs[i][a]);
if (czy_wsp(obs[i], dl[i], prz)) {
nzbior(obs[i], dl[i], prz, n);
}
if (prz[0][prz[0].size() - 1].k == n) {
cout << i;
wyn = true;
break;
}
}
if (!wyn)
cout << m;
return EXIT_SUCCESS;
}
spróbowałem sam coś napisać czytelniej i trochę w inny sposób, jednak mój kod nie przechodzi wszytkich testów, czy ktoś mógłby mi wytłumaczyć jak rozwiązać to zadanie i gdzie robię błąd ?
Mój kod:
#include <bits/stdc++.h>
using namespace std;
class Interval{
public:
int beg;
int end;
Interval(int beg=0, int end=0){
this->beg = beg;
this->end = end;
}
};
bool can_meet(vector<int> & drag_watch, int d_w_len, vector<Interval> & poss_in, int p_i_len){
if (drag_watch[d_w_len - 1] < poss_in[p_i_len - 1].end)
return true;
int p_i_iter = 0;
for (int d_w_iter = 0; d_w_iter < d_w_len; d_w_iter++){
while (p_i_iter < p_i_len){
if (drag_watch[d_w_iter] >= poss_in[p_i_iter].beg && drag_watch[d_w_iter] <= poss_in[p_i_iter].end){
if (drag_watch[d_w_iter] - 1 >= poss_in[p_i_iter].beg && d_w_iter > 0)
if (drag_watch[d_w_iter] - 1 != abs(drag_watch[d_w_iter - 1]))
return true;
drag_watch[d_w_iter] *= -1;
}
else if (drag_watch[d_w_iter] > poss_in[p_i_iter].beg){
if (d_w_iter == 0)
return true;
if (abs(drag_watch[d_w_iter - 1]) != poss_in[p_i_iter].end && drag_watch[d_w_iter - 1] < 0)
return true;
else if (drag_watch[d_w_iter] > poss_in[p_i_iter].end &&
drag_watch[d_w_iter - 1] < poss_in[p_i_iter].end && drag_watch[d_w_iter - 1] > 0)
return true;
}
p_i_iter++;
}
p_i_iter--;
}
return false;
}
void select_all_belonging_to_poss_intervals(vector<int> & drag_watch, int d_w_len, vector<Interval> & poss_in, int p_i_len){
int p_i_iter = 0;
for (int d_w_iter = 0; d_w_iter < d_w_len; d_w_iter++){
while (p_i_iter < p_i_len){
if (drag_watch[d_w_iter] < 0 || drag_watch[d_w_iter] >= poss_in[p_i_iter].beg && drag_watch[d_w_iter] <= poss_in[p_i_iter].end){
drag_watch[d_w_iter] = 0;
break;
}
p_i_iter++;
}
}
}
void update_poss_inters(vector<int> & drag_watch, int d_w_len, vector<Interval> & poss_in, int p_i_len, int last_gnome){
poss_in.clear();
select_all_belonging_to_poss_intervals(drag_watch, d_w_len, poss_in, p_i_len);
if (drag_watch[d_w_len - 1] != last_gnome){
poss_in.push_back(Interval(1, last_gnome));
return;
}
Interval helper;
int d_w_iter = 0;
while (d_w_iter <= d_w_len){
if (d_w_iter == 0)
helper.beg = 1;
else
helper.beg = drag_watch[d_w_iter - 1] + 1;
while (d_w_iter != d_w_len && drag_watch[d_w_iter] == 0)
d_w_iter++;
if (d_w_iter != d_w_len)
helper.end = drag_watch[d_w_iter] - 1;
else
helper.end = last_gnome;
if (helper.beg <= helper.end)
poss_in.push_back(helper);
d_w_iter++;
}
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(nullptr);
int n, m, k, ans;
cin >> n >> m;
ans = m;
vector<vector<int>> dragon_watches(m);
vector<Interval> poss_inters;
poss_inters.push_back(Interval(1,1));
for (int i = 0; i < m; i++){
cin >> k;
dragon_watches[i].reserve(k);
for (int j = 0; j < k; j++)
cin >> dragon_watches[i][j];
if (can_meet(dragon_watches[i], k, poss_inters, poss_inters.size()))
update_poss_inters(dragon_watches[i], k, poss_inters, poss_inters.size(), n);
if (poss_inters[poss_inters.size() - 1].end == n){
ans = i;
break;
}
}
cout << ans;
return 0;
}