Witam, mam zamiar napisać algorytm generujący Krzywą Kocha. Mam tu małe pytanie matematyczne:
Jeśli chcę znaleźć współrzędne wierzchołka trójkąta równobocznego o znanej długości boków to mogę zrobić to tak: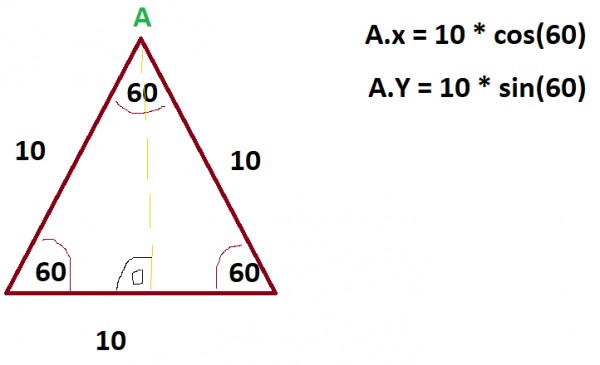
oczywiście sposobów jest wiele. Ten sposób zadziała jednak tylko wtedy kiedy trójkąt będzie w takiej pozycji ( a nie gdy będzie obrócony o jakiś kąt oraz przeniesiony na dowolne miejsce w przestrzeni ). Jak poradzić sobie z tą drugą kwestią?
Pytanie przedstawie może tak:
Znając współrzędne dwóch wierzchołków trójkąta równobocznego o długości boków d, wylicz współrzędne trzeciego niewiadomego wierzchołka.
Wiem że pytanie może być mylące bo nie do końca wiadomo o jaki kąt obrócony jest trójkąt i "czy postawić współrzędne tego wierzchołka za czy przed odcinkiem tworzącym znaną podstawę figury"... Myślę więc że ważna jest kwestia o jaki kąt jest obrócony trójkąt. I tego też nie jestem pewny jak wyliczyć :/
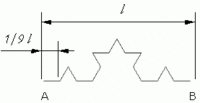
jak widać na powyższym obrazku punkty wierzchołków określamy na odcinkach o różnych nachyleniach. Intuicyjnie wydaje mi się że wszystkie odcinki w dalszych procesach iteracji są nachylone 60 lub 120 stopi względem odcinka |AB|.
Jeśli to jest prawda to z problemem umiem sobie poradzić a jeśli nie to jak wyliczyć wierzchołki ( górne ) każdego z tych pół "trójkątów"?
Wiem że są to podstawy matmy, ale "głupi jest się tylko raz...". Będę więc bardzo wdzięczny za pomoc :)