Wykrywanie kolizji - Separating axis theorem

Question

Dobry wieczór, szukam pomocy przy wykrywaniu kolizji za pomocą Separating axis theorem. 
Sens i sposób działania SAT jest mi znany, utknąłem jednak na matematyce/fizyce przy pisaniu kodu.

Ogólnie korzystam z tego poradnika: SAT PORADNIK i oraz z tego filmu: VIDEO. 

Moja sytuacja wygląda tak: 

Kwadrat, czyli gracz pozostaje w ruchu, linia jest nie ruchoma ale podana rotacji (rotacja gacza się nie zmienia, rotacja linii jest generowana na początku gry). 

Postępując zgodnie z filmem:
1.Znaleźć wektor krawędzi - gotowe
2.Obliczyć wektor normalny - gotowe
3.Projekcja wierzchołków na wektor normalny - to właśnie tu utknąłem.
4.Wyznaczyć min i max
[... ]

Mam wektor [X, Y], od niego wektor normalny [Y, -X], i wektor jednostkowy, mam także współrzędne punktów tylko nie wiem teraz jak obliczyć ich projekcje na tym wektorze. Dużo czytałem na tema SAT, rozumiem czym są wektory, iloczyn wektorowy czy iloczyn skalarny - mimo tego mam problem z obliczeniem tych współrzędnych.

Będę wdzięczny za pomoc, prosił bym tylko o nie podawanie gotowych linków, niestety nie jestem w stanie na ich przykładzie rozwiązać tego problemu. Z góry dziękuje za pomoc. :)
 

Answer 1

Mamy wektor normalny AB o współrzędnych:

A = (x1,y1)
B = (x2,y2)

Na ten wektor możemy nałożyć prostą o równaniu:

y = ax + b

Której współczynniki a, b możemy wyznaczyć jednoznacznie za pomocą współrzędnych wektora, rozwiązując elementarny układ równań:

y1 = ax1 + b
y2 = ax2 + b

Teraz musimy zrzutować na tą prostą wszystkie wierzchołki kwadratu. Jedyne co mamy to równanie prostej. Wiemy jednak, że rzutowanie wierzchołków odbywa się prostopadle do prostej y = ax + b. Wybierzmy sobie jeden z wierzchołków, na przykład A (nie mylić ze współrzędną wektora, którego już nie będziemy dalej używać), którego współrzędne oznaczymy:

A = (xA, yA)

W pierwszej kolejności musimy znaleźć prostą prostopadłą do prostej y = ax + b, która przechodzi przez punkt A:

# Równanie prostej prostopadłej do y = ax + b:
y = -(1/a)x + b'

# Prosta ma przechodzić przez punkt A:
yA = -(1/a)xA + b'
b' = yA + xA/a

Wyznaczyliśmy drugą prostą y = cx + d, gdzie c = -1/a. Mamy więc znowu prosty układ równań z którego możemy wyznaczyć punkt wspólny obu prostych:

y = ax + b
y = cx + d

Znajdując analogicznie pozostałe punkty wspólne dla reszty zrzutowanych wierzchołków, otrzymamy cień kwadratu padający na prostą y = ax + b.

Comments

Trochę to bardziej skomplikowane... i pierwszy raz słyszę o równaniu prostej. 
To jest jedne ze sposobów, tak?

Pytam bo jesteś pierwszą osobą która o tym wspomina...

Najczęściej są jakieś artykuły o iloczynie skalarnym: np 
SAT

---

Trochę to bardziej skomplikowane... i pierwszy raz słyszę o równaniu prostej. 

To wszystko jest tym samym, tylko zapisane inaczej. Na przykład na rysunku prosta y = ax + b jest tożsama z prostą P, gdyby tylko ją przesunąć tak, by pokrywała się z jednym z wektorów normalnych. Proste y = cx + d, to czerwone przerywane linie kreskowane  - - -. Wspólne punkty wyznaczane z ostatniego układu równań, to punkty leżące tam gdzie box1.min, box1.max, box2.min, box2.max (gdyby prosta była przesunięta tak, by pokrywała się z jednym z wektorów normalnych).

---

Możliwe, nie wiem czy to zadziała, mam chwilę czasu spróbuje to dzisiaj napisać - mimo wszystko dzięki wielkie.

---

" Której współczynniki a, b możemy wyznaczyć jednoznacznie za pomocą współrzędnych wektora, rozwiązując elementarny układ równań "

Zacząłem od niebieskiej krawędzi tego kwadratu, i napotkałem na pierwszy problem:

A = (50, 150)
B = (150, 150)

W (wektor) = [X, Y] = [100, 0],
N (wektor normalny) = [Y, -X] = [0, -100]

y = ax + b
150 = 50a + b
150 = 150a + b
z czego możemy wyliczyć równanie prostej y = 0 x + 150 (a = 0, b = 150)...
W tym momencie nie wiem co dalej :(

---

Ok, tutaj jest faktycznie problem, bo pionowa linia prosta (prostopadła do y = ax +b) nie jest funkcją, ponieważ dla jednego argumentu przyjmuje wiele wartości. W takim przypadku odwołałbym się do geometrii, choćby do twierdzenia Pitagorasa. Poza tym popełniłeś błąd, bo użyłeś wektora AB, a nie jest to wektor normalny. Jak znajdę chwilę czasu, to przyjrzę się zapisowi wektorowemu i postaram się to opisać tak, byś zrozumiał jak tego użyć.

---

Przeszukując internet znalazłem jeszcze coś takiego, próbuje to na razie zastosować w praktyce, może tobie się do czegoś przyda.

http://stackoverflow.com/questions/20957749/how-to-project-a-polygon-on-an-axis

---

Nie bardzo rozumiem po co męczyć się z równaniami konkretnych prostych skoro wystarczy nam sam wektor kierunkowy..

---

Spotkałem się pierwszy raz z tym problem, bo nigdy wcześniej nie był mi on potrzebny, i znalazłem rozwiązanie na kolanie. Po przemyśleniach doszedłem do wniosku, że operowanie na wektorach jest prostsze. Opisałem to więc raz jeszcze w kolejnej wiadomości. Niemniej jednak to jest czysta matematyka i oba podejścia dadzą zawsze ten sam wynik. Sposób z wektorami jest łatwiejszy do implementacji w kodzie.

Answer 2

Przeanalizowałem zagadnienie raz jeszcze i wybór wektorów wydaje się prostszy, zwłaszcza jak mamy łatwy dostęp do wierzchołków figur za pomocą metod.

TEORIA

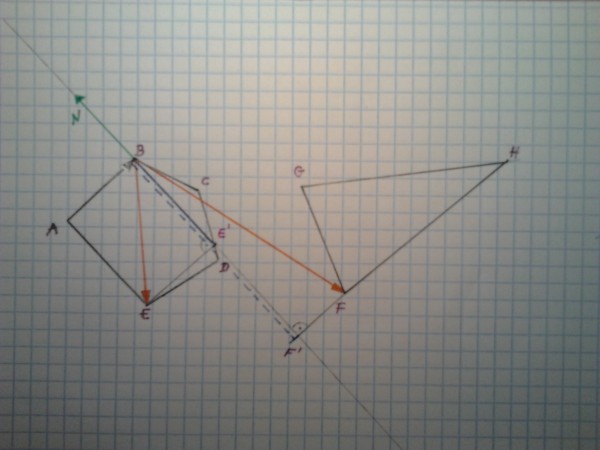
Mamy dwie figury, pięciokąt oraz trójkąt (zobacz rysunek poniżej). Wybieramy jeden z boków, ja wybrałem odcinek |AB|. Obliczamy wektor o początku A i końcu B, oraz liczymy dla niego wektor normalny* N (zielony) zgodnie z tym, co napisałeś w pierwszej wiadomości. Wektor N zaczepiamy w dowolnym punkcie. Ja wybrałem punkt B, równie dobrze mógłby to być punkt A lub dowolny inny. Ważne jest, by ten punkt łatwo dało się wyznaczyć, ponieważ względem niego będziemy wyznaczać pozostałe wektory. Tak więc nasz układ jest zaczepiony w punkcie B. Teraz trzeba by zrzutować każdy z wierzchołków obu figur na prostą, która pokrywa się z wektorem N. Z oczywistych względów nie będziemy rzutować punktów A oraz B, pozostaje więc 6 wierzchołków: C, D, E, F, G, H.

W takim razie tworzymy wektory zaczepione w punkcie B. Na rysunku są dwa takie wektory BE oraz BF (czerwone). Licząc iloczyn skalarny dla dwóch par wektorów:

• wektor normalny N oraz BE
• wektor normalny N oraz BF

i dzieląc je przez długość wektora N, otrzymamy długości* odcinków |BE'| oraz |BF'| (niebieska ciągła i przerywana linia). Widzimy więc, że oba odcinki się pokrywają, co oznacza że nie jesteśmy w stanie stwierdzić, czy figury się przecinają, czy są odseparowane.

CO DALEJ?

Skoro oba zrzutowane odcinki nie są odseparowane, to taką samą procedurę powtarzamy dla kolejnego boku pięciokąta, np. BC. Należy również pamiętać o tym, że nawet jak sprawdzimy całą figurę i nie dostaniemy odseparowanych odcinków, to musimy zbadać w ten sam sposób drugą figurę.

PROBLEMY

W tekście znajdują się dwie *, które wskazują miejsca, w których pojawią się problemy. Pierwszym z nich jest fakt, że zwrot wektora normalnego N może być przeciwny, co przełoży się na znak iloczynu skalarnego. Drugi to fakt, że zrzutowane odcinki, wynikające z iloczynu skalarnego, mogą mieć wartości ujemne. Oczywiście iloczyn skalarny to nie jest długość zrzutowanego odcinka. Jest nią wartość bezwzględna z iloczynu skalarnego, podzielona przez długość wektora N. Oba te zagadnienia będą mieć wpływ na wartości min, max. Spróbuj przemyśleć rozwiązanie tego problemu, który jest także wspomniany na tej stronie.

Comments

Dopiero dzisiaj miałem czas nad tym posiedzieć.

Projekcje obliczane są poprawnie, wszystko się zgadza z tym co rozpisałeś.
Dzięki wielkie za do tych czasowa pomoc.

Posunąłem się już trochę do przodu ale dalej utknąłem, a to już prawie końcówka projektu.

"Widzimy więc, że oba odcinki się pokrywają, co oznacza że nie jesteśmy w stanie stwierdzić, czy figury się przecinają, czy są odseparowane."

"Oba te zagadnienia będą mieć wpływ na wartości min, max. "

Jak byś miał jakieś wskazówki jak to zrobić w kodzie to będę bardzo wdzięczny.

---

Spójrz raz jeszcze na rysunek. Skupmy się na pierwszej figurze. Projekcja którego wierzchołka da najdłuższy wektor? Według mnie będzie to wierzchołek D, a więc najdłuższy odcinek (pierwsza figura) to będzie |BD'|, czyli:

max = |BD'|

Teraz analizujemy trójkąt. Projekcja wierzchołka G da nam najkrótszy wektor:

min = |BG'|

Oba odcinki są zaczepione w tym samym punkcie, tak więc wystarczy porównać ich długości. Jeśli zajdzie:

min > max

to oznacza to, że figury są odseparowane i możemy przerwać dalsze sprawdzanie. Nawiązując do mojej poprzedniej wiadomości, problem z * zostają rozwiązane (długość odcinka to liczba dodatnia). Pełny algorytm wyglądałby tak:

1. Wybieramy pierwszą figurę i dowolny jej bok
2. Liczymy wektor normalny
3. Dla pierwszej figury liczymy długości zrzutowanych odcinków (wartość bezwzględna z iloczynu skalarnego, podzielona przez długość wektora N)
4. Wybieramy najdłuższy odcinek i oznaczamy go jako max
5. Dla drugiej figury liczymy długości zrzutowanych odcinków
6. Wybieramy najkrótszy odcinek i oznaczamy go jako min
7. Porównujemy min z max, jeśli min <= max, to idziemy do 1. i wybieramy kolejny bok, w przeciwnym razie kończymy sprawdzanie, ponieważ figury są odseparowane

Myślę, że jak zrozumiesz jak to działa, to bez problemu poradzisz sobie z implementacją w kodzie.

---

bool colision(sf::RectangleShape & box1, sf::VertexArray & box, sf::RenderWindow & win)
{
	
	sf::Vector2f point1[4], point2[2];

	// wierzchołki kwadratu
	for (int i = 0; i < 4; i++)
	{
		point1[i] = box1.getTransform().transformPoint(box1.getPoint(i)); 
	}

	// wierzchołki lini
	for (int i = 0; i < 2; i++)
	{
		point2[i] = box[i].position; 
	}

	sf::Vector2f vector, normal;
	float projection1[4];
	float projection2[2];

	// sprawdzam wierzchołki kwadratu
	for (int x = 0; x < 4; x++)
	{
		// wektory kwadratu
		if (x == 3)
		{
			vector = getVector(point1[x], point1[0]);
		}
		else
		{
			vector = getVector(point1[x], point1[x + 1]);
		}

		// wektor normalny 
		normal = getNormalVector(vector);

		// projekcie punktów kwadratu na wektor norlmany 
		for (int y = 0; y < 4; y++)
		{
			projection1[y] = abs(dot(normal, getVector(point1[x], point1[y])) / getVectorLenght(normal));
		}

		// sortowanie
		std::sort(projection1, projection1 + 4);

		float max = projection1[3];

		// projekcie punktów lini na wektor norlmany 
		for (int y = 0; y < 2; y++)
		{
			projection2[y] = abs(dot(normal, getVector(point1[x], point2[y])) / getVectorLenght(normal));
		}

		std::sort(projection2, projection2 + 2);

		float min = projection2[0];

		if (min <= max)
		{
			// brak wolnych kraweżi sprawdzam dalej
		}
		else
		{
			// wolna krawędź
			return false;
		}
	}

	// wierzchołki lini

	for (int x = 0; x < 2; x++)
	{
		// wektor lini
		if (x == 0)
			vector = getVector(point2[x], point2[x + 1]);
		else
			vector = getVector(point2[x], point2[x - 1]);

		// wektor normalny 
		normal = getNormalVector(vector);

		// projekcie punktów kwadratu na wektor norlmany 
		for (int y = 0; y < 4; y++)
		{
			projection1[y] = abs(dot(normal, getVector(point2[x], point1[y])) / getVectorLenght(normal));
		}

		// sortowanie
		std::sort(projection1, projection1 + 4);

		float min = projection1[0];


		// projekcie punktów lini na wektor norlmany 
		for (int y = 0; y < 2; y++)
		{
			projection2[y] = abs(dot(normal, getVector(point2[x], point2[y])) / getVectorLenght(normal));
		}

		std::sort(projection2, projection2 + 2);

		float max = projection2[1];

		if (min <= max)
		{
			// brak wolnych krawezi sprawdzamy algorytm dalej 
		}
		else
		{
			// wolna krawędź 
			return false;
		}
	}

	// brak wolnych krawezi 

	return true;

}

Na ten moment algorytm nie działa poprawnie, rozpisałem sobie wszystko i doszedłem do wniosku gdzie występuje problem. Przy projekcji linii na jej wektor normalny wynik zawsze będzie równy 0 (linia jest prostopadła do wektora normalnego, z definicji wiemy jednak że w takim wypadku iloczyn skalarny jest równy zero). 

Przy sprawdzaniu kwadratu wszystko jest jak najbardziej w porządku, tak jak wspomniałem wyżej pojawiają się problemy z drugą figurą.

Schemat operacji:

1.Obliczam wektor linii
2. Obliczam wektor normalny
3. Rzutuje wszystkie wierzchołki linii na wektor normalny i wyznaczam max (wykonuje te wszystkie inne obliczenia co opisałeś wyżej) - wynik zawsze równy zero
4 Rzutuje wierzchołki kwadratu na wektor normalny i wyznaczam min (wykonuje te wszystkie inne obliczenia co opisałeś wyżej) - wynik zawsze jest większy od zera 

W związku z czym max < min Figury są odseparowane, nawet jeżeli są wewnątrz siebie. 
Pod uwagę należy więc wziąć drugi etap algorytmu - sprawdzania osi figury drugiej. 

Na dzień dzisiejszy nie mam pomysły jak to obejść, w związku z czym (o ile to jeszcze możliwe) liczę na twoją pomoc. 

Całość dostępna no moim githubie: https://github.com/Craix/SAT-FORUM 



 

---

Przy projekcji linii na jej wektor normalny wynik zawsze będzie równy 0 (...)

Tak jak napisałem w poście, który teraz komentujemy, rozwiązanie z wektorami jest prostsze niż rozwiązanie z liniami, które wymyśliłem na szybko na samym początku. Linia prosta na rysunku jest tylko pomocnicza, byś widział jak poszczególne wektory rzutują się na wektor normalny N. Innymi słowy w tym zagadnieniu operujemy już tylko wektorami. Gdy popatrzymy na rysunek w wiadomości, to zauważymy że tylko iloczyn skalarny wektora N z wektorem AB da nam 0. Dla pozostałych iloczynów skalarnych:

• N • (BC)
• N • (BD)
• N • (BE)
• N • (BF)
• N • (BG)
• N • (BH)

wartości muszą być różne od 0, gdzie • oznacza iloczyn skalarny. Rozbij sobie program na mniejsze elementy i napisz kod odpowiedzialny za następujące zadanie:

Dla dowolnej figury o N wierzchołkach wybierz wierzchołki i=1 oraz j=2. Z tych wierzchołków skonstruuj wektor oraz wektor do niego normalny. Następnie skonstruuj N-2 wektorów, z których każdy jest zaczepiony w wierzchołku j=2, a ich końce są zaczepione odpowiednio w wierzchołkach k=3, 4, ... , N. Następnie policz iloczyny skalarne tych wektorów z wektorem normalnym.

Jeśli wyjdą Ci same 0, to wklej ten kod odpowiedzialny tylko za to zadanie. Na razie nie martw się drugą figurą.

---

Od samego początku pod uwagę brałem przykład z wektorami, chodziło mi raczej że  druga z figur jest linią - patrz obrazek w temacie. 

Kod prezentuje się tak:
projekcje wierzchołków kwadratu na wektor normalny liczony z wektorów kwadratu:

W pętli liczę wektory kolejnych krawędzi, z tego wektor normalny i projekcje - które zapisuje do tablicy - potem wybieram max - odcinek o największej długości to samo robię z drugim obiektem w moim wypadku z linią z tym że obliczam min, po czym porównuję min i max.

Wszystko zgodnie z tym co opisałeś w punktach. 

 

	for (int x = 0; x < 4; x++)
	{
		// wektory kwadratu
		if (x == 3)
		{
			vector = getVector(point1[x], point1[0]);
		}
		else
		{
			vector = getVector(point1[x], point1[x + 1]);
		}

		// wektor normalny 
		normal = getNormalVector(vector);

		// projekcie punktów kwadratu na wektor norlmany 
		for (int y = 0; y < 4; y++)
		{
			projection1[y] = abs(dot(normal, getVector(point1[x], point1[y])) / getVectorLenght(normal));
		}

		// sortowanie
		std::sort(projection1, projection1 + 4);

		float max = projection1[3];

		// projekcie punktów lini na wektor norlmany 
		for (int y = 0; y < 2; y++)
		{
			projection2[y] = abs(dot(normal, getVector(point1[x], point2[y])) / getVectorLenght(normal));
		}

		std::sort(projection2, projection2 + 2);

		float min = projection2[0];

		if (min <= max)
		{
			// brak wolnych kraweżi sprawdzam dalej
		}
		else
		{
			// wolna krawędź
			return false;
		}
	}

 

        Schemat:
        0. Wybieramy objekt  pierwszy 
        1. Liczymy wektor krawędzi 
        2. Liczymy wektor normalny 
        3. Projekcje punktów na wektor normalny objektu wybranego, sortujemy i oznaczamy największy jako max
        4. Liczymy projkcje punktów drugiego obiektu, sortujemy i wyznaczamy min 
        5. Porównujemy mix i max jesli min <= max, to iziemy do punktu pierwszego (zapętlamy), jeśli tak to przerywamy objekty są odseparowane.
        W innym wypadku sprawdzamy kolejne krawedzie, jeśli dla żadna z nich nie jest odseparowana 
        (czyli sprawdziliśmy wszystkie krawędzie) objekty na siebie zachodzą - jest kolizja. 

        Sprawdzamy objekt pierwszy i drugi - wszystkie krawędzie.

 

---

Zrobiłem jeden przykład na kartce i polecam Tobie też przerobienie tego przykładu, bo gdzieś brakuje Ci pewnej informacji (domyślam się gdzie, ale bez konkretnego przypadku będzie mi ciężko to wyjaśnić). Na kartce w kratkę narysuj sobie pierwszą ćwiartkę układu współrzędnych XY. Nanieś na nią dwa trójkąty ABC oraz DEF, które są odseparowane. Konkretne punkty (te co u mnie) to:

• A = (2,2)
• B = (7,5)
• C = (3,9)
• D = (10,6)
• E = (17,5)
• F = (15,11)

Wykonujemy instrukcje zgodnie z tym, co napisałem wyżej:

1. Wybieramy pierwszą figurę i dowolny jej bok
   Wybrałem bok AC trójkąta ABC. Wektor AC = [3-2,9-2] = [1,7]
2. Liczymy wektor normalny
   N = [7,-1], a jego długość |N| = sqrt(7*7 + (-1)*(-1)) = 5*sqrt(2)
3. Dla pierwszej figury liczymy długości zrzutowanych odcinków (wartość bezwzględna z iloczynu skalarnego, podzielona przez długość wektora N)
   Jak pisałem gdzieś wyżej, wektor N może być zaczepiony w którymkolwiek punkcie. Wybrałem sobie punkt A. Widzimy więc, że dla pierwszej figury  będziemy rzutować tylko jeden wektor, mianowicie wektor AB, ponieważ zrzutowanie wektora AC na wektor normalny nie ma sensu, bo wynik będzie równy 0. AB = [7-2,5-2] = [5,3].
   |AB * N| / |N| = |5*7 + (-1)*3| / 5*sqrt(2) = 3.2*sqrt(2)
4. Wybieramy najdłuższy odcinek i oznaczamy go jako max
   Ponieważ dla pierwszej figury istnieje tylko jedna zrzutowana wartość, to jest to szukane max = 3.2*sqrt(2)
5. Dla drugiej figury liczymy długości zrzutowanych odcinków (myślę że tu masz problem)
   Rozpatrujemy drugą figurę, a więc wektory AD = [8,4], AE = [15,3], AF = [13,9]. I dalej
   |AD * N| / |N| = 5.2*sqrt(2)
   |AE * N| / |N| = 10.2*sqrt(2)
   |AF * N| / |N| = 8.2*sqrt(2)
6. Wybieramy najkrótszy odcinek i oznaczamy go jako min
   min = 5.2*sqrt(2)
7. Porównujemy min z max, jeśli min <= max, to idziemy do 1. i wybieramy kolejny bok, w przeciwnym razie kończymy sprawdzanie, ponieważ figury są odseparowane
   min > max, a więc figury są odseparowane

Spróbuj sobie przerobić to zadanie. Specjalnie dobrałem odseparowane trójkąty, by liczyć mało wektorów i w pierwszym warunku wyjść z pętli, kończąc procedurę. Ty możesz spróbować sobie policzyć przypadek, gdy trójkąty nachodzą na siebie.

---

Postępowałem zgodnie z twoimi zaleceniami.

Wybrałem dwa kwadraty - podany rotacji i nie podany rotacji oraz sytuację w której zachodzi kolizja. Udało mi się stworzyć algorytm do wykrywania kolizji i jest on w pełni sprawny.

(koda dodam wkrótce na gihtuba lub wstawię w komentarzu)

Algorytmu tego niestety nie można odnieść do sytuacji którą opisałem w pierwszy poście zakładając ten temat - kolizja kwadratu i odcinka.

Jeszcze raz proszę więc abyś zwrócił uwagę konkretnie na ten przypadek i związane z tym nowe problemy.

Jestem ci bardzo wdzięczny za wszystkie rady i poświęcony czas, pozdrawiam.

Przykład z odcinkiem:

Kwadrat:
A (2,5)
B (2,3)
C (4,3)
D (4,5)

Odcinek:
E (2,6)
F (5,3)

AB = [0,2]
N = [2, - 0]

AA = 0
AB = 0
AC = 2
AD = 2
MAX = 2.

AE = 0
AF = 3.
MIN = 3

MIN > MAX - według algorytmu nie zachodzą w rzeczywistości występuje jednak kolizja.

---

MIN = 0, a nie 3 ;)

Answer 3

Projekcja figury na oś to po prostu policzenie iloczynu skalarnego (dot product) każdego z wierzchołków (punkt, czyli jakby wektor przesunięcia od punktu {0, 0}) z osią (jej wektorem kierunkowym) i z uzyskanych wyników wybranie najmniejszego i największego. Te dwie wybrane wartości są projekcją.

Nie przyglądałem się za bardzo podesłanemu przez ciebie poradnikowi, ale być może ten będzie przystępniejszy. Być może warto też tutaj zajrzeć.

Comments

Jak masz jakieś uwagi lub rady to będę bardzo wdzięczny.

Staram się tylko zrozumieć jak działa ten algorytm, i jak go zastosować w swoim projekcie :)

---

Raaczej nie. Tyle, co ci te linki podesłałem. Sam niewiele wiem na ten temat. Wykorzystywałem ten algorytm, ale nadal tak troche po omacku :D

---

I tak dzięki :)

Jak każda pomoc mi się przyda, jak na razie mam naprawdę niewiele.
http://pastebin.com/YQa8N9L6

Answer 4

Podsumowując owoc mojej prawie miesięcznej pracy. 

Pierwsza wersja została już napisana i działa jak najbardziej poprawnie. Wykrywanie kolizji pomiędzy dwoma kwadratami nie zależnie od rotacji.

Dla zainteresowanych kod na moim githubie: [SFML 2.x] [C/C++] 
https://github.com/Craix/SAT/blob/forum/rec.cpp
Wersja nie jest jeszcze zoptymalizowana ani tym bardziej skończona. 

Druga sprawa... przykład z trójkątami.

A = 2,2
B = 4 2
C = 2 4
D = 5 2
E = 5 4
F = 3 4

Mam dwa trójkąty ABC i DEF w widoczny sposób są one od siebie odseparowane.  



Opis algorytmu: 
1. Wybieramy krawędź pierwszej z figur i liczymy wektor normalny oraz jego długość.
2. Rzutujemy odcinki pierwszej figury i wybieramy max oraz rzutujemy odcinki drugiej figury i wybieramy min.
3. Porównujemy max i min -> jeśli min > max figury są odseparowane 

Rzutujemy zgodnie ze wzorem: wartość bezwzględna z iloczynu skalarnego ((wektor normalny x inny wektor) podzielona przez długość wektora normalnego. 

OBLICZENIA

AB = 2,0 
NAB = 0, -2 
|AB| = 2 

AA = 0
AB = 0
AC = 2
MAX = 2
AD = 0
AE = 2
AF = 2
MIN = 0 
MAX > MIN - nie odseparowane

BC = -2 2 
NBC = 2 2
|BC| = 2*sqrt(2) **

BA = 2 
BB = 0
BC = 0
MAX = 2 
BD = 1
BE = 3 
BF = 1 
MIN = 1
MAX > MIN - nie odseparowane 

**wszystkie wartości należy jeszcze podzielić przez sqrt(2) nie zmienia to jednak faktu że figury są odseparowane a jedynie utrudnia licznie (uwzględniłem to jednak w swoich obliczeniach i wynik jest ten sam)


CA = 0 -2
NCA = -2, 0
|CA| = 2 

CA = 0
CB = 2
CC = 0
MAX = 2
CD = 3
CE = 3
CF = 1
MIN = 1
MAX > MIN - nie odseparowane 

DRUGA FIGURA


DE = 0 2
NDE = 2 0
|DE| = 2

DA = 3
DB = 1
DC = 3
MIN = 1 
DD = 0
DE = 0
DF = 2
MAX = 2
MAX > MIN - nie odseparowane 

EF = -2 0
NEF = 0 2
|EF| = 2 

EA = 2 
EB = 2
EC = 0
MIN = 0
ED = 2
EE = 0
EF = 0
MAX = 2
MAX > MIN - nie odseparowane

FD = 2 -2
NFD = -2 -2
|FD| = 2 * sqrt(2) **

FA = 3
FB = 1
FC = 1
MIN = 1
FD = 0
FE = 2
FF = 0
MAX = 2 

MAX > MIN - nie odseparowane 

**wszystkie wartości należy jeszcze podzielić przez sqrt(2) nie zmienia to jednak faktu że figury są odseparowane a jedynie utrudnia licznie (uwzględniłem to jednak w swoich obliczeniach i wynik jest ten sam)


Zgodnie z tymi obliczeniami figury ABC i DEF nie są odseparowane co jest stwierdzeniem błędnym... Zostawiam dal chętnych do analizy, ja z tym problemem walczę dalej :) Jak tylko uda mi się na coś jeszcze wpaść dam znać dla potomnych. 

Answer 5

Rzutowanie wektora prostopadle na wektor: http://obliczeniowo.com.pl/?id=172

Innymi słowy rzutujesz współrzędne wierzchołków twojego kwadratu na wektor normalny N.